1 Intro to Spatial Data

In the workshop, we learned about:

• What is Spatial Data?
• What is the sf framework for R?

To delve in further, let’s see some spatial data in action.

We’ll work with the sf library first.

library(sf)

1.1 Load Spatial Data

First load in the shapefile. Remember, this type of data is actually comprised of multiple files. All need to be present in order to read correctly.

Chi_tracts = st_read("data/geo_export_aae47441-adab-4aca-8cb0-2e0c0114096e.shp")

## Reading layer `geo_export_aae47441-adab-4aca-8cb0-2e0c0114096e' from data source 
##   `/Users/maryniakolak/Code/Intro2RSpatialMed/data/geo_export_aae47441-adab-4aca-8cb0-2e0c0114096e.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 801 features and 9 fields
## Geometry type: POLYGON
## Dimension:     XY
## Bounding box:  xmin: -87.94025 ymin: 41.64429 xmax: -87.52366 ymax: 42.02392
## Geodetic CRS:  WGS84(DD)

1.2 Non-Spatial & Spatial Views

Always inspect data when loading in. First we look at a non-spatial view.

head(Chi_tracts)

## Simple feature collection with 6 features and 9 fields
## Geometry type: POLYGON
## Dimension:     XY
## Bounding box:  xmin: -87.68822 ymin: 41.72902 xmax: -87.62394 ymax: 41.87455
## Geodetic CRS:  WGS84(DD)
##   commarea commarea_n countyfp10     geoid10 name10        namelsad10 notes statefp10 tractce10
## 1       44         44        031 17031842400   8424 Census Tract 8424  <NA>        17    842400
## 2       59         59        031 17031840300   8403 Census Tract 8403  <NA>        17    840300
## 3       34         34        031 17031841100   8411 Census Tract 8411  <NA>        17    841100
## 4       31         31        031 17031841200   8412 Census Tract 8412  <NA>        17    841200
## 5       32         32        031 17031839000   8390 Census Tract 8390  <NA>        17    839000
## 6       28         28        031 17031838200   8382 Census Tract 8382  <NA>        17    838200
##                         geometry
## 1 POLYGON ((-87.62405 41.7302...
## 2 POLYGON ((-87.68608 41.8229...
## 3 POLYGON ((-87.62935 41.8528...
## 4 POLYGON ((-87.68813 41.8556...
## 5 POLYGON ((-87.63312 41.8744...
## 6 POLYGON ((-87.66782 41.8741...

Note the last column – this is a spatially enabled column. The data is no longer a ‘shapefile’ but an `sf’ object, comprised of polygons.

We can use a baseR function to view the spatial dimension. The sf framework enables previews of each attribute in our spatial file.

plot(Chi_tracts)

1.3 Spatial Data Structure

Check out the data structure of this file… What object is it?

str(Chi_tracts)

## Classes 'sf' and 'data.frame':   801 obs. of  10 variables:
##  $ commarea  : chr  "44" "59" "34" "31" ...
##  $ commarea_n: num  44 59 34 31 32 28 65 53 76 77 ...
##  $ countyfp10: chr  "031" "031" "031" "031" ...
##  $ geoid10   : chr  "17031842400" "17031840300" "17031841100" "17031841200" ...
##  $ name10    : chr  "8424" "8403" "8411" "8412" ...
##  $ namelsad10: chr  "Census Tract 8424" "Census Tract 8403" "Census Tract 8411" "Census Tract 8412" ...
##  $ notes     : chr  NA NA NA NA ...
##  $ statefp10 : chr  "17" "17" "17" "17" ...
##  $ tractce10 : chr  "842400" "840300" "841100" "841200" ...
##  $ geometry  :sfc_POLYGON of length 801; first list element: List of 1
##   ..$ : num [1:243, 1:2] -87.6 -87.6 -87.6 -87.6 -87.6 ...
##   ..- attr(*, "class")= chr [1:3] "XY" "POLYGON" "sfg"
##  - attr(*, "sf_column")= chr "geometry"
##  - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA NA NA NA NA
##   ..- attr(*, "names")= chr [1:9] "commarea" "commarea_n" "countyfp10" "geoid10" ...

Check out the coordinate reference system. What is it? What are the units?

st_crs(Chi_tracts)

## Coordinate Reference System:
##   User input: WGS84(DD) 
##   wkt:
## GEOGCRS["WGS84(DD)",
##     DATUM["WGS84",
##         ELLIPSOID["WGS84",6378137,298.257223563,
##             LENGTHUNIT["metre",1,
##                 ID["EPSG",9001]]]],
##     PRIMEM["Greenwich",0,
##         ANGLEUNIT["degree",0.0174532925199433]],
##     CS[ellipsoidal,2],
##         AXIS["geodetic longitude",east,
##             ORDER[1],
##             ANGLEUNIT["degree",0.0174532925199433]],
##         AXIS["geodetic latitude",north,
##             ORDER[2],
##             ANGLEUNIT["degree",0.0174532925199433]]]

1.4 Exploring Coordinate Reference Systems

Lets see how switching CRS changes our object. First we’ll try the Mollweide coordinate reference system that does a good job preserving area across the globe.

To transform our CRS, we use the st_transform function. To plot, we use baseR again but with some paremeter updates. Finally, we check out the CRS of our new object. What are the units? Any other details to note? Will this be appropriate for our spatial analysis?

Chi_tracts.moll <- st_transform(Chi_tracts, crs="ESRI:54009")

plot(st_geometry(Chi_tracts.moll), border = "gray", lwd = 2, main = "Mollweide", sub="preserves areas")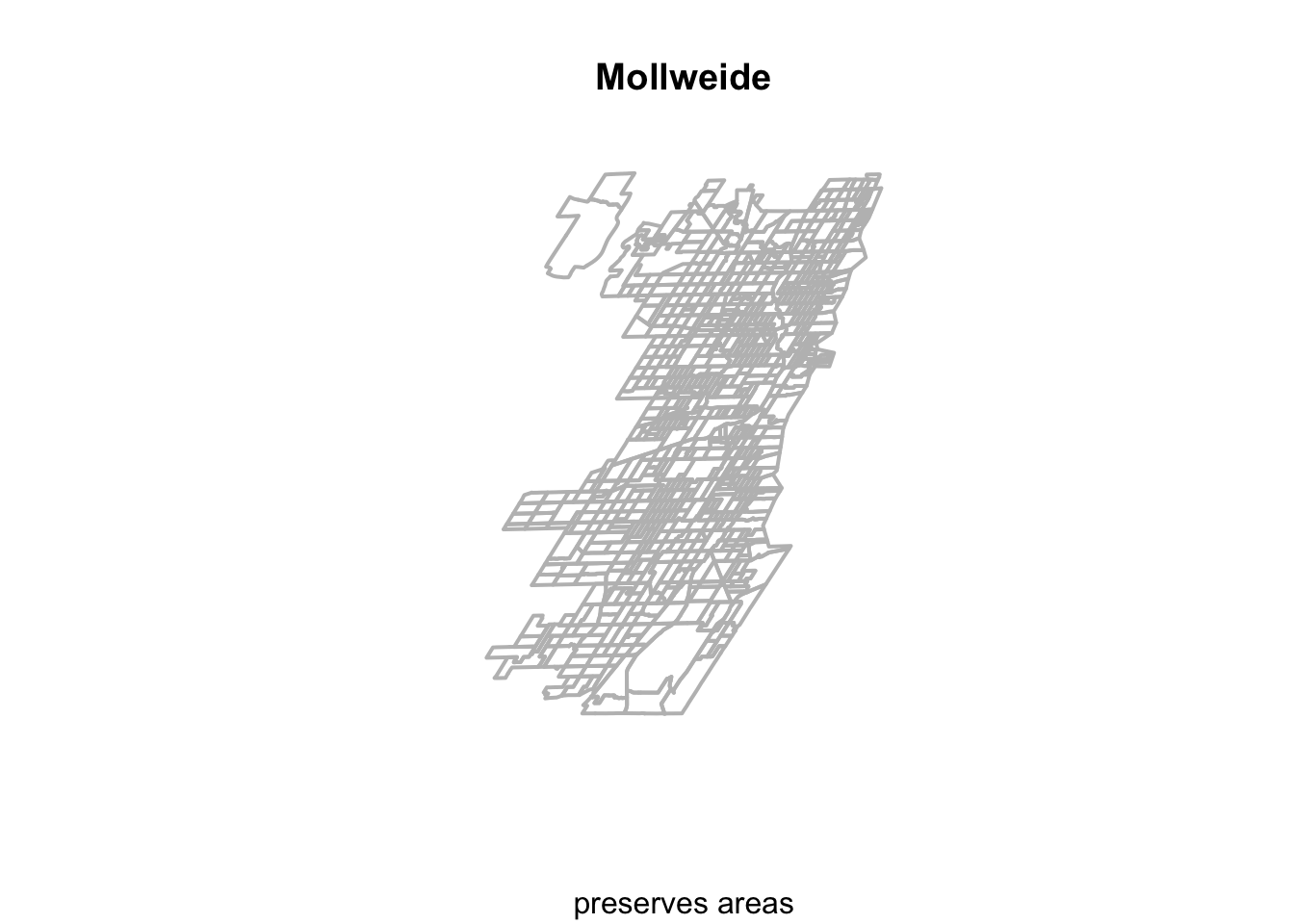

st_crs(Chi_tracts.moll)

## Coordinate Reference System:
##   User input: ESRI:54009 
##   wkt:
## PROJCRS["World_Mollweide",
##     BASEGEOGCRS["WGS 84",
##         DATUM["World Geodetic System 1984",
##             ELLIPSOID["WGS 84",6378137,298.257223563,
##                 LENGTHUNIT["metre",1]]],
##         PRIMEM["Greenwich",0,
##             ANGLEUNIT["Degree",0.0174532925199433]]],
##     CONVERSION["World_Mollweide",
##         METHOD["Mollweide"],
##         PARAMETER["Longitude of natural origin",0,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8802]],
##         PARAMETER["False easting",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8806]],
##         PARAMETER["False northing",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8807]]],
##     CS[Cartesian,2],
##         AXIS["(E)",east,
##             ORDER[1],
##             LENGTHUNIT["metre",1]],
##         AXIS["(N)",north,
##             ORDER[2],
##             LENGTHUNIT["metre",1]],
##     USAGE[
##         SCOPE["Not known."],
##         AREA["World."],
##         BBOX[-90,-180,90,180]],
##     ID["ESRI",54009]]

Next, we’ll try the Winkel CRS, which is a compromise projection that facilitates minimal distortion for area, distance, and angles. We use the same approach, recyling the code with new inputs.

Chi_tracts.54019 = st_transform(Chi_tracts, crs="ESRI:54019")
plot(st_geometry(Chi_tracts.54019), border = "gray", lwd = 2, main = "Winkel", sub="minimal distortion")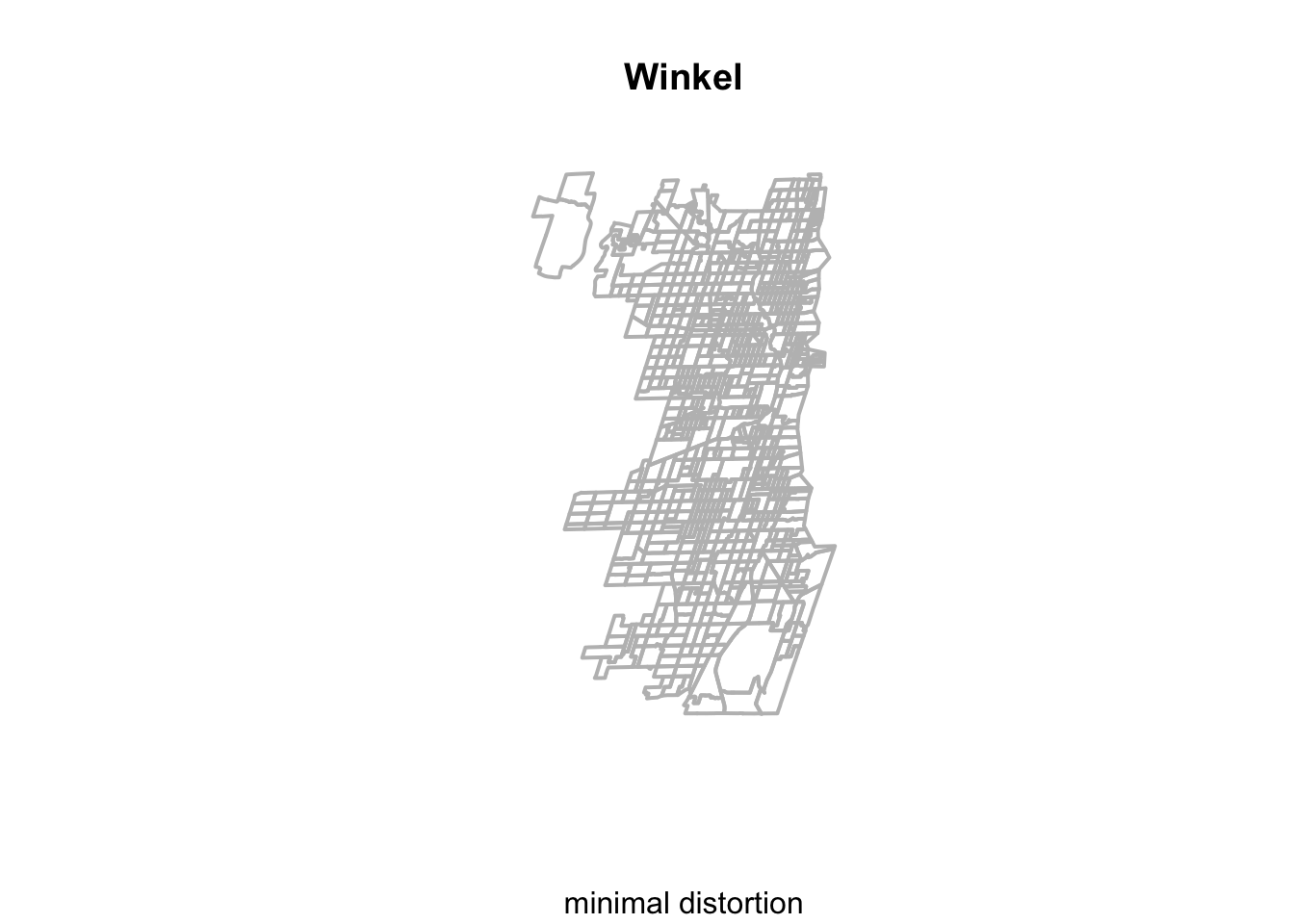

st_crs(Chi_tracts.54019)

## Coordinate Reference System:
##   User input: ESRI:54019 
##   wkt:
## PROJCRS["World_Winkel_II",
##     BASEGEOGCRS["WGS 84",
##         DATUM["World Geodetic System 1984",
##             ELLIPSOID["WGS 84",6378137,298.257223563,
##                 LENGTHUNIT["metre",1]]],
##         PRIMEM["Greenwich",0,
##             ANGLEUNIT["Degree",0.0174532925199433]]],
##     CONVERSION["World_Winkel_II",
##         METHOD["Winkel II"],
##         PARAMETER["Longitude of natural origin",0,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8802]],
##         PARAMETER["Latitude of 1st standard parallel",50.4597762521898,
##             ANGLEUNIT["Degree",0.0174532925199433],
##             ID["EPSG",8823]],
##         PARAMETER["False easting",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8806]],
##         PARAMETER["False northing",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8807]]],
##     CS[Cartesian,2],
##         AXIS["(E)",east,
##             ORDER[1],
##             LENGTHUNIT["metre",1]],
##         AXIS["(N)",north,
##             ORDER[2],
##             LENGTHUNIT["metre",1]],
##     USAGE[
##         SCOPE["Not known."],
##         AREA["World."],
##         BBOX[-90,-180,90,180]],
##     ID["ESRI",54019]]

We could also try a totally different projection, to see how that changes our spatial object. Let’s use the “Old Hawaiian UTM Zone 4n” projection, with the EPSG identified from an online search. How does this fare?

Chi_tracts.Hawaii = st_transform(Chi_tracts, crs="ESRI:102114")
plot(st_geometry(Chi_tracts.Hawaii), border = "gray", lwd = 2, main = "Old Hawaiian UTM Zone 4N", sub="wrong projection!")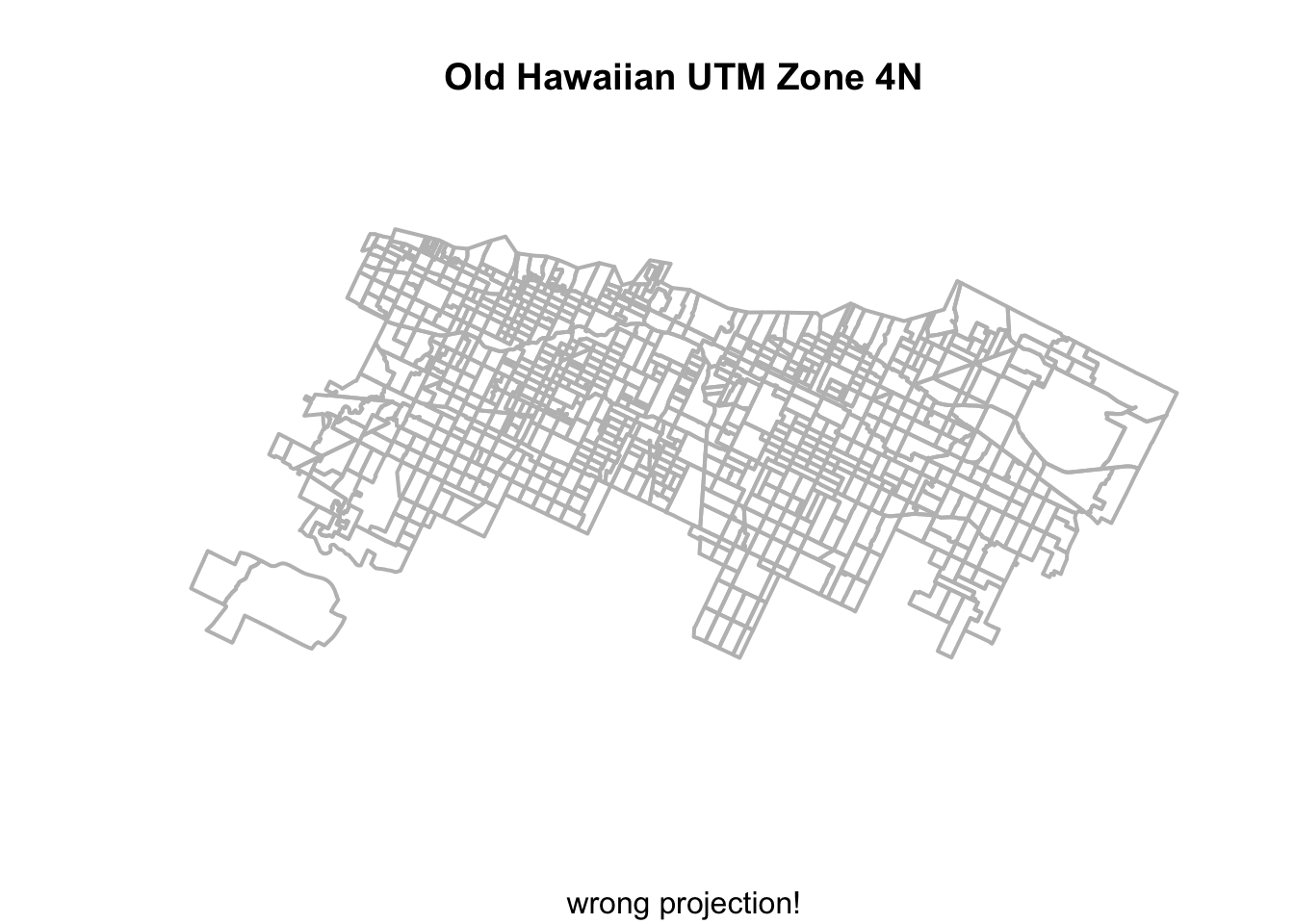

Finally.. let’s choose a projection that is focused on Illinois, and uses distance as feet or meters, to make it a bit more accessible for our work. EPSG:3435 is a good fit:

Chi_tracts.3435 <- st_transform(Chi_tracts, "EPSG:3435")
# Chi_tracts.3435 <- st_transform(Chi_tracts, 3435)
st_crs(Chi_tracts.3435)

## Coordinate Reference System:
##   User input: EPSG:3435 
##   wkt:
## PROJCRS["NAD83 / Illinois East (ftUS)",
##     BASEGEOGCRS["NAD83",
##         DATUM["North American Datum 1983",
##             ELLIPSOID["GRS 1980",6378137,298.257222101,
##                 LENGTHUNIT["metre",1]]],
##         PRIMEM["Greenwich",0,
##             ANGLEUNIT["degree",0.0174532925199433]],
##         ID["EPSG",4269]],
##     CONVERSION["SPCS83 Illinois East zone (US Survey feet)",
##         METHOD["Transverse Mercator",
##             ID["EPSG",9807]],
##         PARAMETER["Latitude of natural origin",36.6666666666667,
##             ANGLEUNIT["degree",0.0174532925199433],
##             ID["EPSG",8801]],
##         PARAMETER["Longitude of natural origin",-88.3333333333333,
##             ANGLEUNIT["degree",0.0174532925199433],
##             ID["EPSG",8802]],
##         PARAMETER["Scale factor at natural origin",0.999975,
##             SCALEUNIT["unity",1],
##             ID["EPSG",8805]],
##         PARAMETER["False easting",984250,
##             LENGTHUNIT["US survey foot",0.304800609601219],
##             ID["EPSG",8806]],
##         PARAMETER["False northing",0,
##             LENGTHUNIT["US survey foot",0.304800609601219],
##             ID["EPSG",8807]]],
##     CS[Cartesian,2],
##         AXIS["easting (X)",east,
##             ORDER[1],
##             LENGTHUNIT["US survey foot",0.304800609601219]],
##         AXIS["northing (Y)",north,
##             ORDER[2],
##             LENGTHUNIT["US survey foot",0.304800609601219]],
##     USAGE[
##         SCOPE["Engineering survey, topographic mapping."],
##         AREA["United States (USA) - Illinois - counties of Boone; Champaign; Clark; Clay; Coles; Cook; Crawford; Cumberland; De Kalb; De Witt; Douglas; Du Page; Edgar; Edwards; Effingham; Fayette; Ford; Franklin; Gallatin; Grundy; Hamilton; Hardin; Iroquois; Jasper; Jefferson; Johnson; Kane; Kankakee; Kendall; La Salle; Lake; Lawrence; Livingston; Macon; Marion; Massac; McHenry; McLean; Moultrie; Piatt; Pope; Richland; Saline; Shelby; Vermilion; Wabash; Wayne; White; Will; Williamson."],
##         BBOX[37.06,-89.28,42.5,-87.02]],
##     ID["EPSG",3435]]

plot(st_geometry(Chi_tracts.3435), border = "gray", lwd = 2, main = "NAD83 / Illinois East (ftUS)", sub="topo mapping & survey use")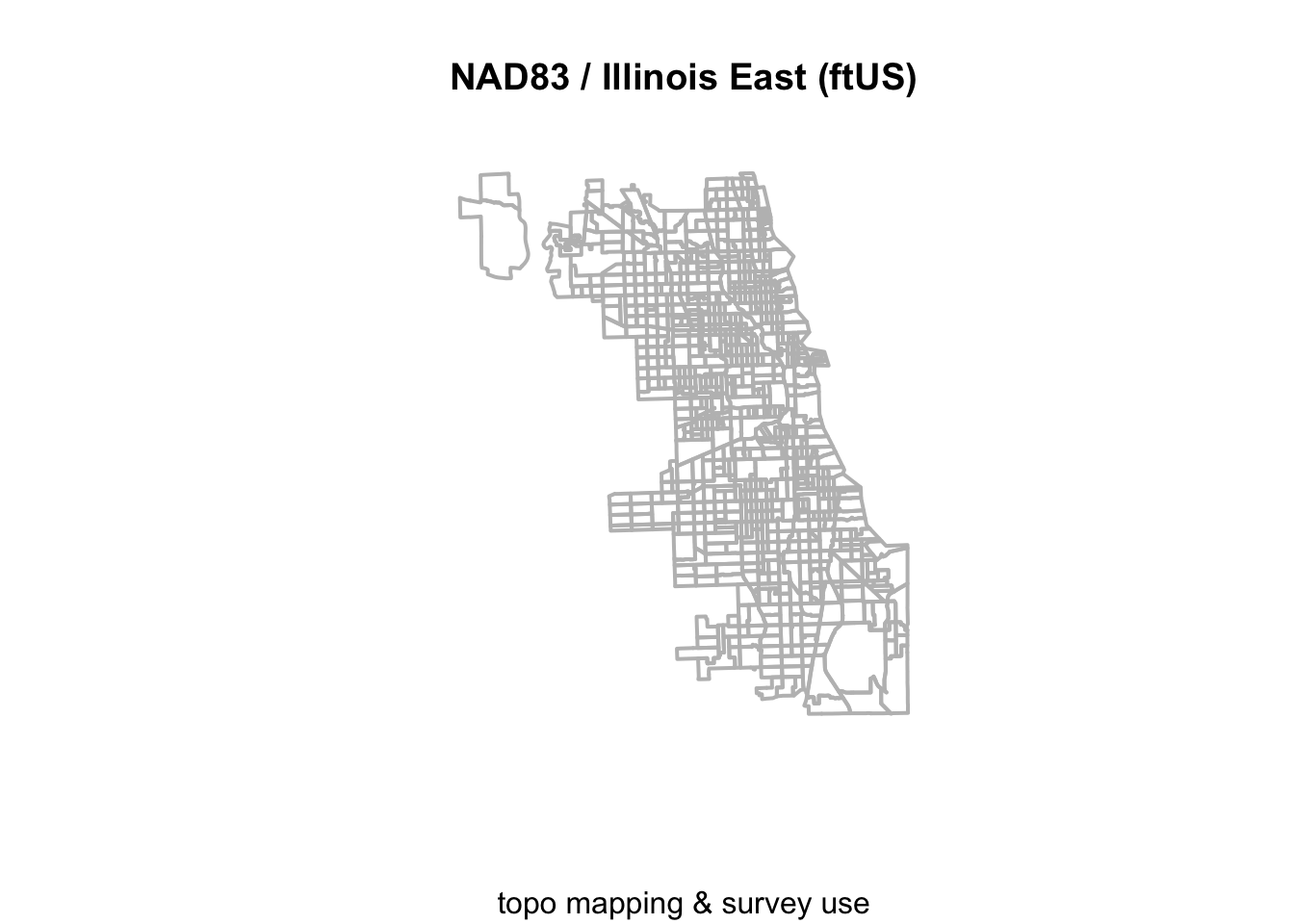

1.5 Refine Basic Map

Now we’ll switch to a more extensive cartographic mapping package, tmap. We approach mapping with one layer at a time. Always start with the object you want to map by calling it with the tm_shape function. Then, at least one descriptive/styling function follows. There are hundreds of variations and paramater specifications, so take your time in exploring tmap and the options.

Here we style the tracts with some semi-transparent borders.

library(tmap)

tm_shape(Chi_tracts) + tm_borders(alpha=0.5)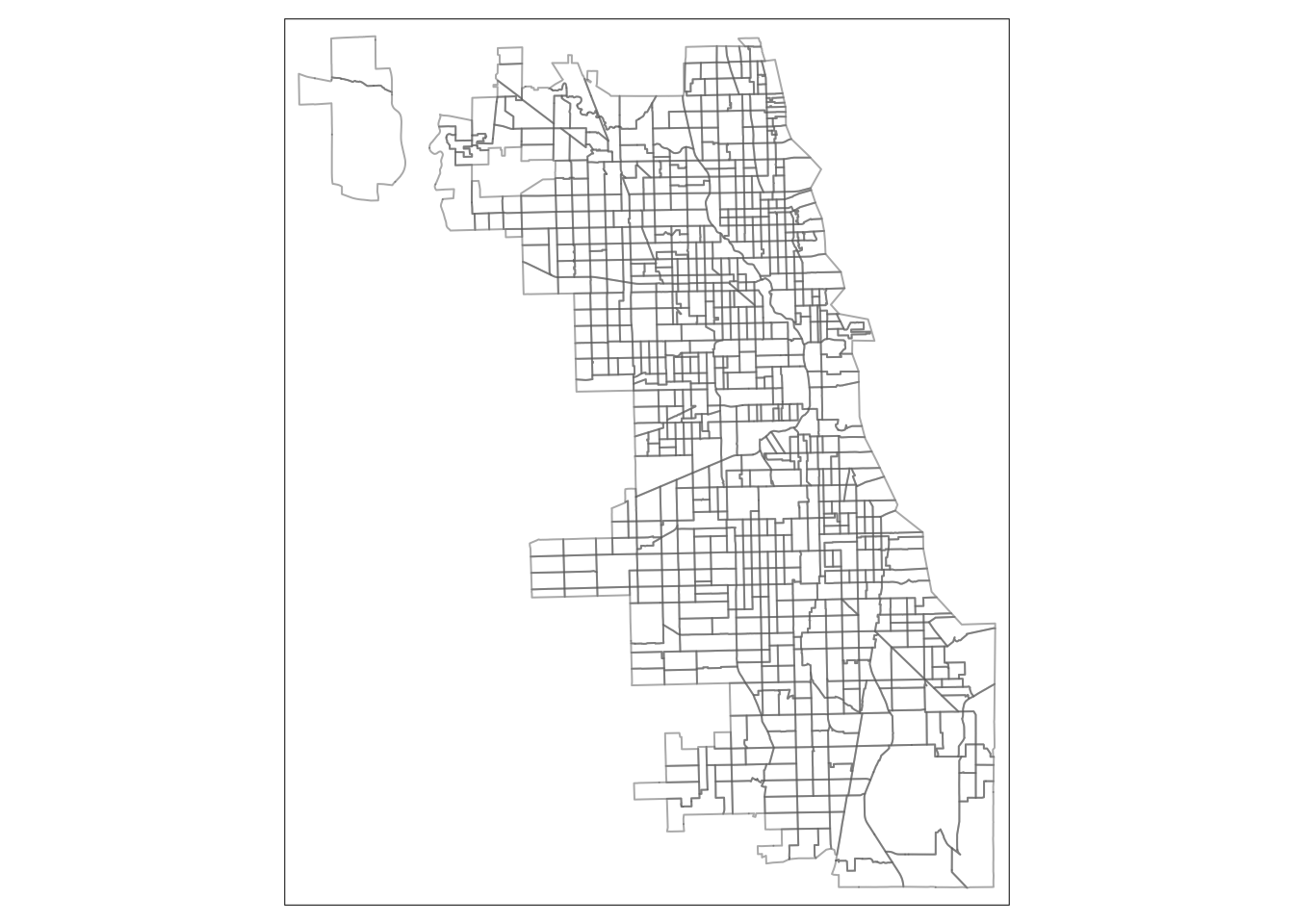 

Next we fill the tracts with a light gray, and adjust the color and transparency of borders. We also add a scale bar, positioning it to the left and having a thickness of 0.8 units, and turn off the frame.

tm_shape(Chi_tracts) + tm_fill(col = "gray90") + tm_borders(alpha=0.2, col = "gray10") +
  tm_scale_bar(position = ("left"), lwd = 0.8) +
  tm_layout(frame = F)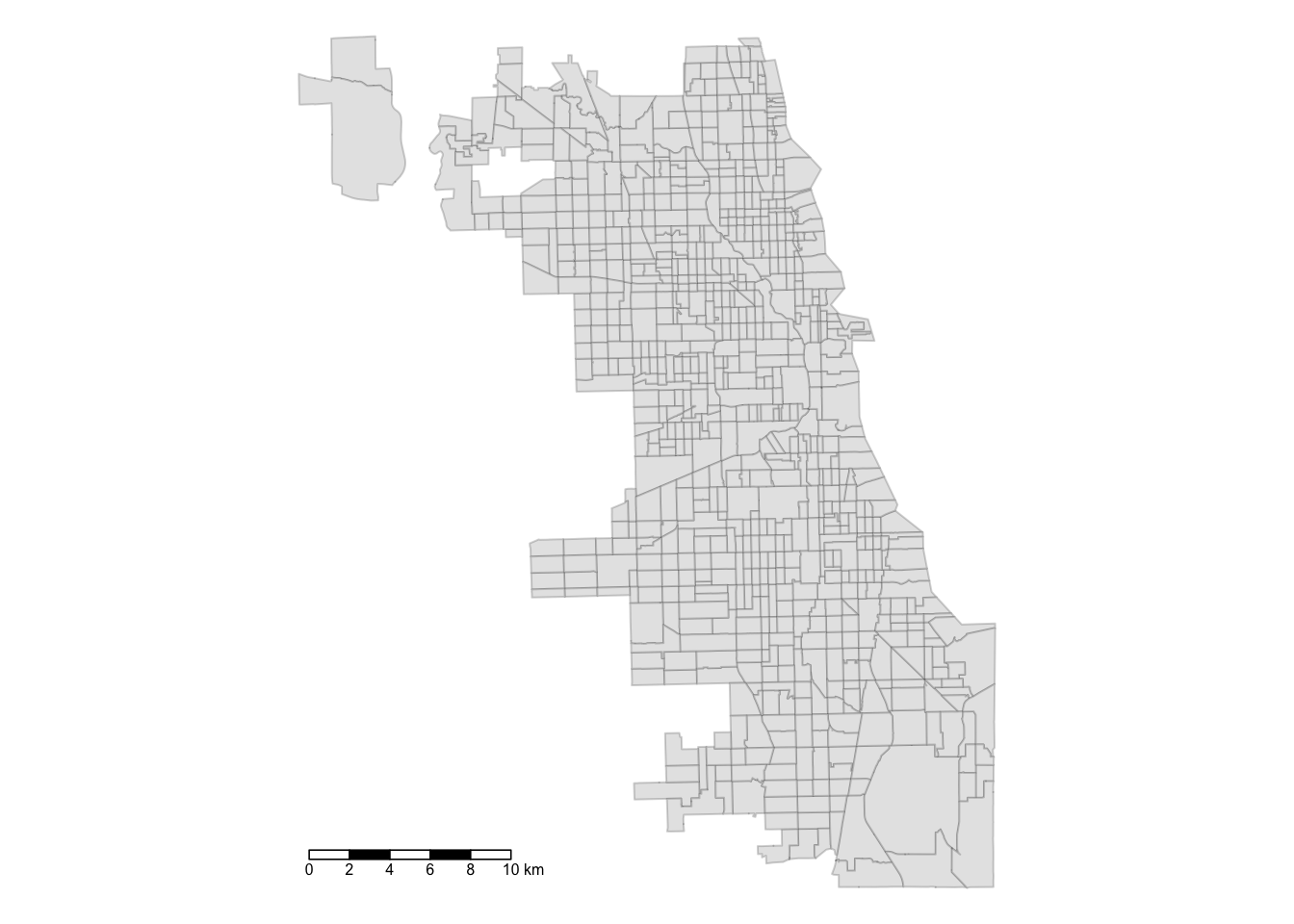

Check out https://rdrr.io/cran/tmap/man/tm_polygons.html for more ideas!

1.6 Arrange multiple maps

Sometimes we want to look at multiple maps at once. Write your mapping function to a new variable, and then call that variable in order of desire using the tmap_arrange function. Hint: this is just one of many! ways to map multiples using tmap… see if you can uncover more in the documentation.

tracts.4326 <- tm_shape(Chi_tracts) + tm_fill(col = "gray90") +
  tm_layout(frame = F, title = "EPSG 4326")

tracts.54019 <- tm_shape(Chi_tracts.54019) + tm_fill(col = "gray90") +  tm_layout(frame = F, title = "EPSG 54019")

tmap_arrange(tracts.4326, tracts.54019)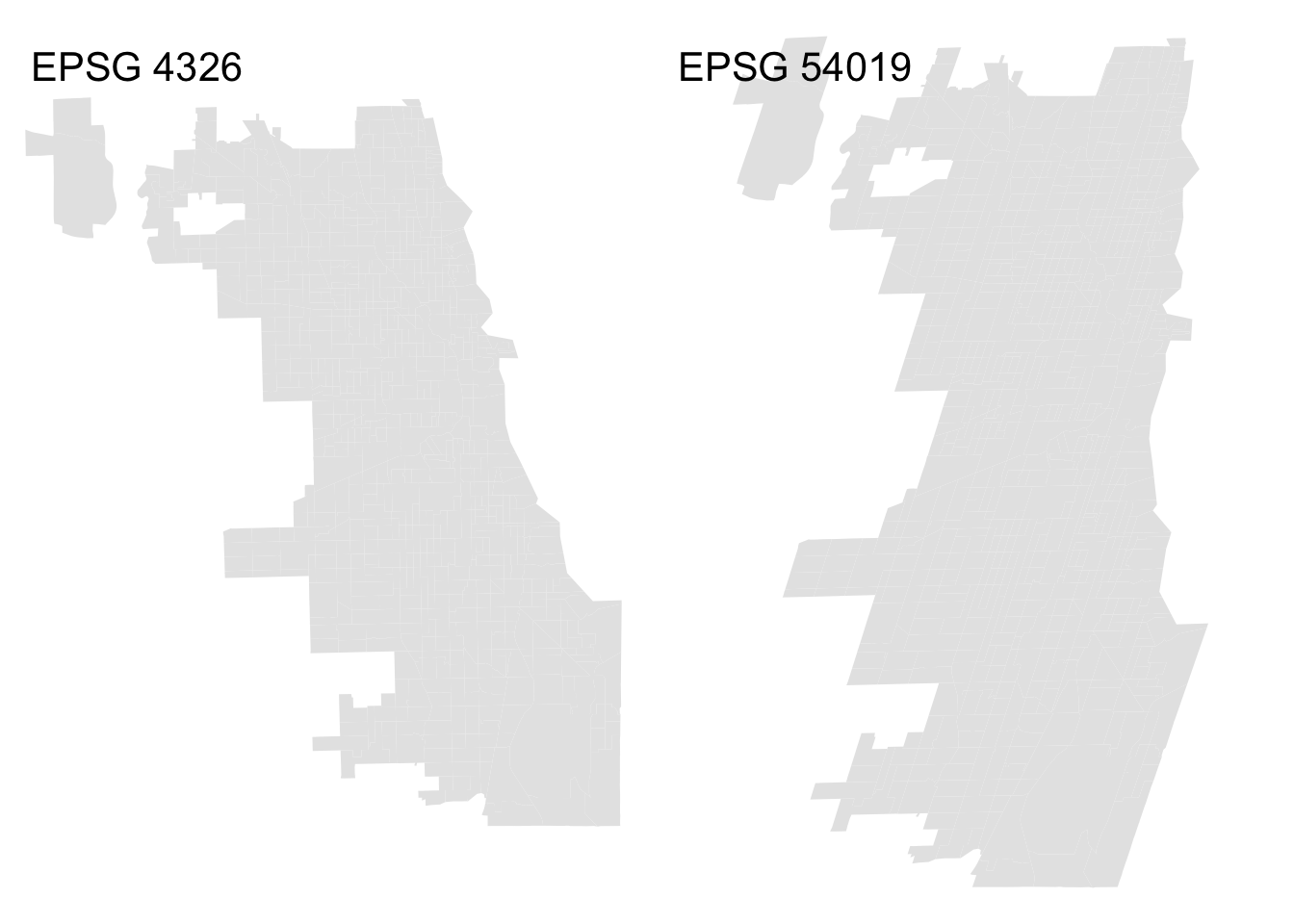

1.7 Interactive Mode

So far, we’ve been plotting static maps. We can also switch to an interactive map that uses a Leaflet widget by switching the tmap_mode() parameter specification from “plot” to “view.” It’s on “plot” as default.

tmap_mode("view")

## tmap mode set to interactive viewing

Map the same map as before, and check out the interaction!

tm_shape(Chi_tracts) + tm_fill(col = "gray90") + tm_borders(alpha=0.2, col = "gray10") +
  tm_scale_bar(position = ("left"), lwd = 0.8) +
  tm_layout(frame = F)

The tracts are not transparent enough, so we update that here. You can also click the box on the left side to try out other basemaps. See if you can find out how to add a basemap to a static/plotted map, using tmap documentation…

tm_shape(Chi_tracts) + tm_fill(col = "gray90", alpha = 0.5) + tm_borders(alpha=0.2, col = "gray10") + tm_scale_bar(position = ("left"), lwd = 0.8) +  tm_layout(frame = F)

We revert back to plot mode for now.

tmap_mode("plot")

## tmap mode set to plotting

1.8 Overlay Zip Code Boundaries

How do census tract areas correspond to zip codes? While tracts better represent neighborhoods, often times we are stuck with zip code level scale in healh research. Here we’ll make a reference map to highlight tract distribution across each zip code.

First, we read in zip code boundaries. This data was downloaded directly from the City of Chicago Data Portal as a shapefile.

Chi_Zips = st_read("data/geo_export_54bc15d8-5ef5-40e4-8f72-bb0c6dbac9a5.shp")

## Reading layer `geo_export_54bc15d8-5ef5-40e4-8f72-bb0c6dbac9a5' from data source 
##   `/Users/maryniakolak/Code/Intro2RSpatialMed/data/geo_export_54bc15d8-5ef5-40e4-8f72-bb0c6dbac9a5.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 61 features and 4 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -87.94011 ymin: 41.64454 xmax: -87.52414 ymax: 42.02304
## Geodetic CRS:  WGS84(DD)

Next, we layer the new shape in – on top of the tracts. We use a thicker border, and try out a new color. Experiment!

## FIRST LAYER: CENSUS TRACT BOUNADRIES
tm_shape(Chi_tracts.3435) + tm_fill(col = "gray90") +
  tm_borders(alpha=0.2, col = "gray10") + 

## SECOND LAYER: ZIP CODE BOUNDARIES WITH LABEL
tm_shape(Chi_Zips) + tm_borders(lwd = 2, col = "#0099CC") +
  tm_text("zip", size = 0.7) +
  
## MORE CARTOGRAPHIC STYLE
  tm_scale_bar(position = ("left"), lwd = 0.8) +
  tm_layout(frame = F)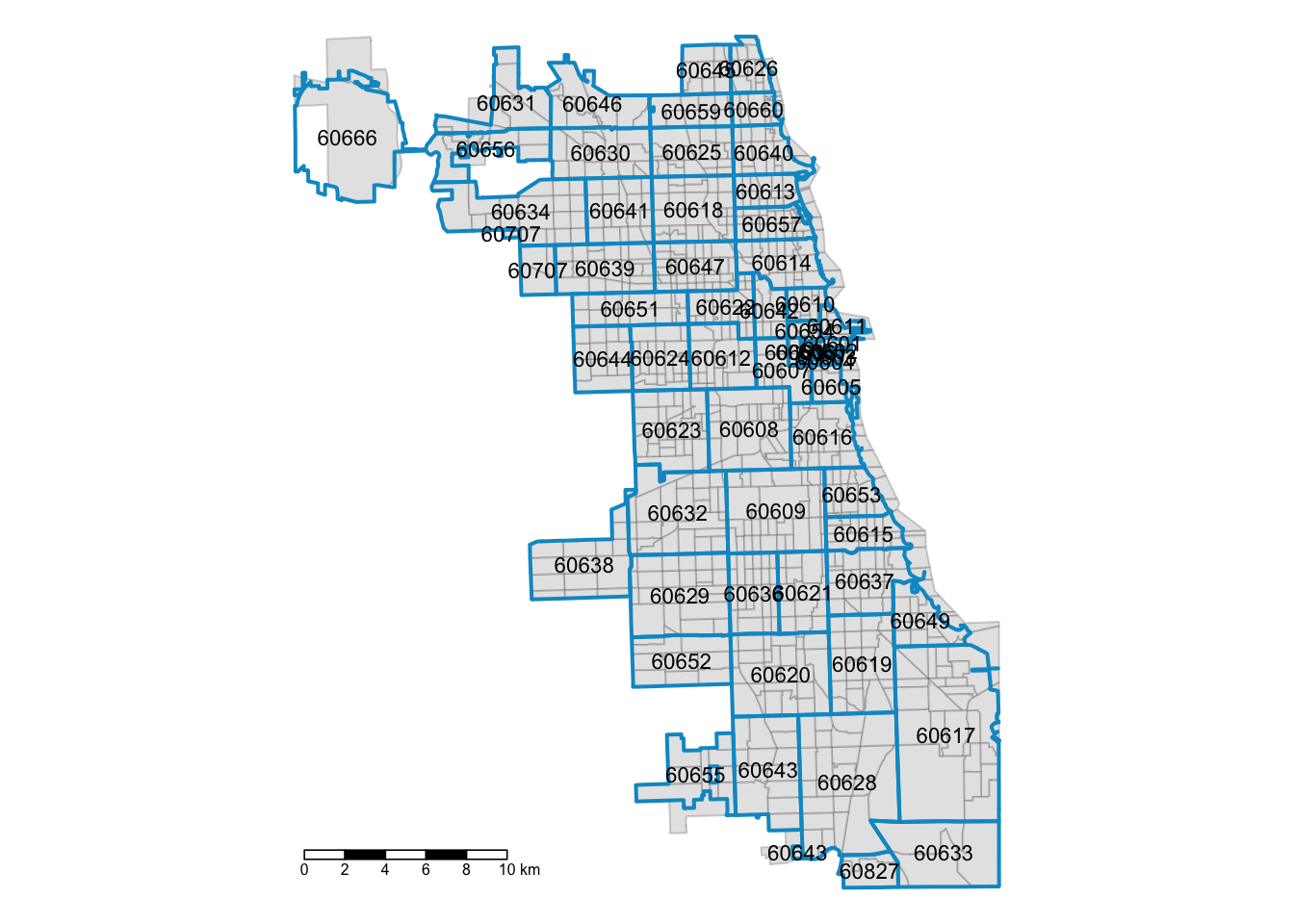

More Resources

On spatial data basics & sf:

• https://geocompr.robinlovelace.net/intro.html

• https://geodacenter.github.io/opioid-environment-toolkit/spatial-data-introduction.html

On projections:

• https://desktop.arcgis.com/en/arcmap/10.3/guide-books/map-projections/projection-basics-for-gis-professionals.htm

• https://geocompr.robinlovelace.net/reproj-geo-data.html

• https://datacarpentry.org/organization-geospatial/03-crs/index.html

On tmap:

• https://cran.r-project.org/web/packages/tmap/vignettes/tmap-getstarted.html

• https://geocompr.robinlovelace.net/adv-map.html